分支定界

考虑下面的 整数规划问题（Integer Programming）。

其中变量 $x_1, x_2$ 的取值为非负整数。

本文介绍整数规划的一种求解思路，称为 分支定界（Branch and Bound）。它是一种搜索的思想。每一个分支代表一种可能性，搜索可能的分支，直到找到最优解。

分支 link

先不考虑整数条件，把原问题看成线性规划。

LP0

它的最优解为 $x^* = (4, 1.5)$。此时 $x_2$ 不是整数。那么它有两种情况：

$$ x_2\leq 1 \text{ \textcolor{red}{or} } x_2\geq 2 $$

这样一来，我们得到两个子问题。

LP1

LP2

分别求解 LP1 和 LP2。重复这样的步骤，直到搜完所有情况，如下图所示。

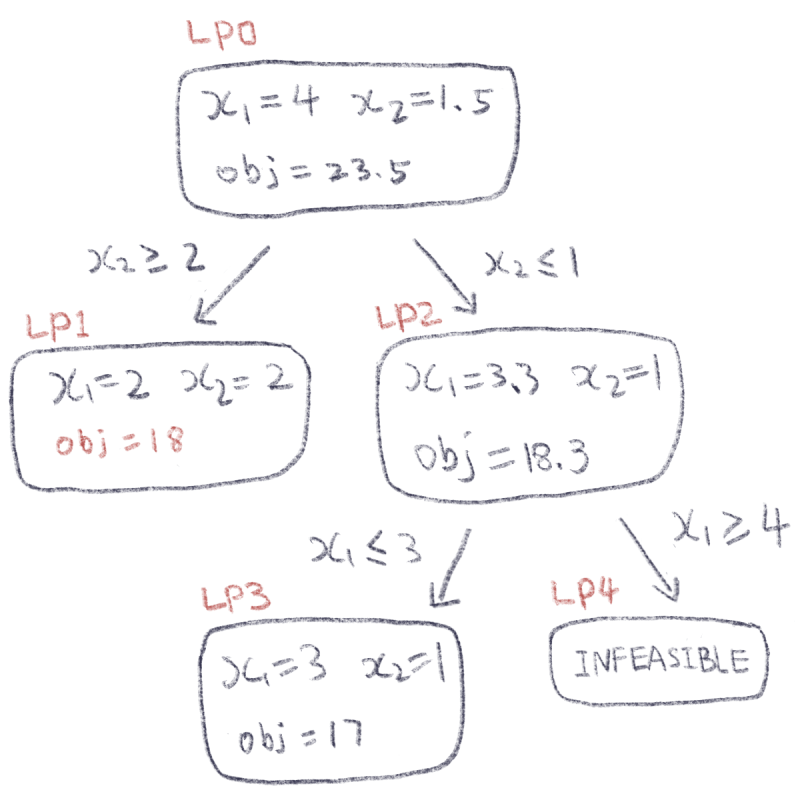
其中目标函数值最大的整数解就是最优解。在这个例子中，最优解是 $x_1=2, x_2=2$，最优目标函数值为 $18$。

定界 link

为了加快搜索效率，可以利用中间计算结果，对最优解的上界或下界进行估计，从而跳过一些分支。

以最大化问题为例。假设原问题存在最优解，其最优目标函数值记作 $\text{opt}$。用 $b$ 记录搜索到的整数解的目标函数值。因此 $b$ 就是 $\text{opt}$ 的下界。如果某个节点的最优目标函数值小于 $b$，意味着它的所有子节点都可以跳过。

具体来说。对某个结点 $i$，其目标函数值记作 $\text{opt}_i$。如果它的最优解是整数解且 $\text{opt}_i > b$，于是更新 $b:= \text{opt}_i $。对某个节点 $j$，如果 $\text{opt}_j < b$。那么节点 $j$ 及其子节点就可以跳过。

算法 link

我们求解的整数规划问题有两个假设：一是最大化问题，二是变量值非负。这个假设主要是为了描述方便。如果是最小化问题，对目标函数值取负号，可以把它转化成最大化问题；如果变量值允许负数，引入辅助变量可以改写为非负。

接下来描述算法。

初始化

• x 记录整数解
• b=-INF 是 x 对应的目标函数值。
• root 是根节点，它是原问题对应的线性规划问题，即不考虑整数约束。

搜索

用 深度优先（Depth First Search） 的方式进行搜索。

从根节点 root 开始，计算它的最优解，如果是分数解，就按上面的方法进行分支得到子问题，用递归的方式对子问题求解，直到子问题是整数解或者子问题无解。

下面是伪代码。

  def depth_first_search(node):

    # 求解当前节点
    x_node, objective_node, status = solve(node)
    
    # 不可行或者无界则返回
    if status is not "OPTIMAL":
        return
    
    # 剪枝
    if objective_node <= b:
        return
        
    # 更新 b 和 x
    if x_node is feasible:
        if objective_node > b:
    	      b = objective
    	      x = x_node
    	  return
    
    # 分支
    child1, child2 = branch(x_node)
    # 递归求解子节点
    depth_first_search(child1)
    depth_first_search(child2)
  

结果

在上面的搜索过程中，b 记录可行解中目标函数值的最大值，x 是对应的整数解。如果原问题存在最优解，搜索结束后 x 就是最优解，b 就是最优目标函数值。